Annualized Return Calculator

Calculate the annualized return rate to evaluate investment performance over time.

Please fill in all the fields.

What is Annualized Return?

Annualized Return is the geometric average amount of money earned by an investment each year over a given time period.

Annualized Return represents the compound annual growth rate (CAGR) that smooths out returns over time, making it easier to compare investments.

Understanding Annualized Return helps investors evaluate and compare the performance of different investments on a standardized annual basis.

This metric is particularly useful for comparing investments with different time horizons, as it normalizes returns to an annual percentage.

Annualized Return assumes that returns are compounded annually and that the investment grows at a steady rate over the entire period.

The calculation is based on the total return from beginning to end of the investment period, regardless of interim fluctuations.

Annualized Return should be used alongside other metrics like volatility and maximum drawdown for comprehensive investment analysis.

Annualized Return Formula

\begin{gather*}\bold{Given{:}}\newline\begin{aligned}\text{Final Value} &= \mathrm{FV}\newline\text{Initial Investment} &= \mathrm{IC}\newline\text{Time Period in Years} &= \mathrm{t}\end{aligned}\newline\bold{Calculate{:}}\newline\text{Annualized Return} = \mathrm{AR} \newline = ((\frac{\mathrm{FV}}{\mathrm{IC}})^{\frac{1}{\mathrm{t}}} - 1) \times \mathrm{100{\%}}\end{gather*}

Annualized Return Calculation Examples

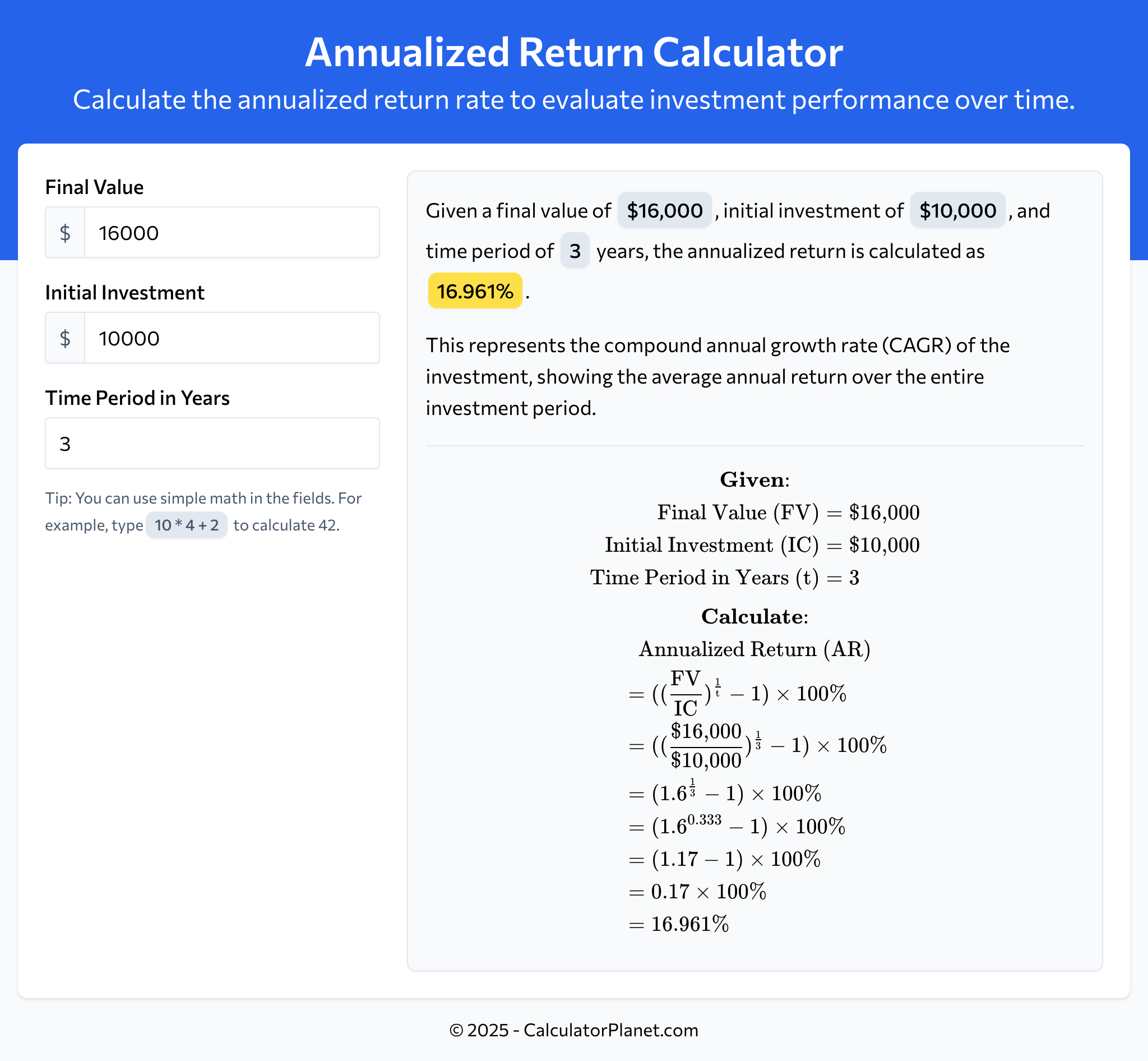
Example 1

A venture capital firm invests $10,000 in a startup and expects to receive $16,000 when they exit the investment after 3 years.

To evaluate the attractiveness of this investment:

\begin{gather*}\bold{Given{:}}\newline\begin{aligned}\text{Final Value}\space(\mathrm{FV}) &= \mathrm{{\$}16{,}000}\newline\text{Initial Investment}\space(\mathrm{IC}) &= \mathrm{{\$}10{,}000}\newline\text{Time Period in Years}\space(\mathrm{t}) &= 3\end{aligned}\newline\bold{Calculate{:}}\newline\text{Annualized Return}\space(\mathrm{AR})\newline\begin{aligned}&= ((\frac{\mathrm{FV}}{\mathrm{IC}})^{\frac{1}{\mathrm{t}}} - 1) \times \mathrm{100{\%}}\newline&= ((\frac{\mathrm{{\$}16{,}000}}{\mathrm{{\$}10{,}000}})^{\frac{1}{3}} - 1) \times \mathrm{100{\%}}\newline&= (1.6^{\frac{1}{3}} - 1) \times \mathrm{100{\%}}\newline&= (1.6^{0.333} - 1) \times \mathrm{100{\%}}\newline&= (1.17 - 1) \times \mathrm{100{\%}}\newline&= 0.17 \times \mathrm{100{\%}}\newline&= \mathrm{16.961{\%}}\end{aligned}\end{gather*}

The annualized return is 16.961%, meaning the investment generates an annualized return of 16.961%.

This return rate can be compared to the firm's required rate of return to determine if the investment meets their profitability criteria.

Example 2

An investor purchases rental property for $20,000 and plans to sell it for $25,000 after 5 years of ownership.

Let's calculate the annualized return for this real estate investment:

\begin{gather*}\bold{Given{:}}\newline\begin{aligned}\text{Final Value}\space(\mathrm{FV}) &= \mathrm{{\$}25{,}000}\newline\text{Initial Investment}\space(\mathrm{IC}) &= \mathrm{{\$}20{,}000}\newline\text{Time Period in Years}\space(\mathrm{t}) &= 5\end{aligned}\newline\bold{Calculate{:}}\newline\text{Annualized Return}\space(\mathrm{AR})\newline\begin{aligned}&= ((\frac{\mathrm{FV}}{\mathrm{IC}})^{\frac{1}{\mathrm{t}}} - 1) \times \mathrm{100{\%}}\newline&= ((\frac{\mathrm{{\$}25{,}000}}{\mathrm{{\$}20{,}000}})^{\frac{1}{5}} - 1) \times \mathrm{100{\%}}\newline&= (1.25^{\frac{1}{5}} - 1) \times \mathrm{100{\%}}\newline&= (1.25^{0.2} - 1) \times \mathrm{100{\%}}\newline&= (1.046 - 1) \times \mathrm{100{\%}}\newline&= 0.0456 \times \mathrm{100{\%}}\newline&= \mathrm{4.564{\%}}\end{aligned}\end{gather*}

The annualized return is 4.564%, indicating that this property investment generates an annualized return of 4.564%.

This return rate helps the investor compare this opportunity against other investments and determine if it meets their return expectations.

Reference This Page

If you found our Annualized Return Calculator valuable, please consider referencing this page in your work. You can easily cite it by using the following formatted text:

<a href="https://calculatorplanet.com/finance/annualized-return">Annualized Return Calculator by Calculator Planet</a>

Annualized Return Calculator by CalculatorPlanet.com