Compound Annual Growth Rate (CAGR) Calculator

Calculate the compound annual growth rate of an investment.

Please fill in all the fields.

What is Compound Annual Growth Rate (CAGR)?

Compound Annual Growth Rate (CAGR) is the rate at which an investment grows annually over a specified period, assuming the investment grows at a steady rate.

CAGR is calculated by taking the final value of the investment, dividing it by the initial value, raising the result to the power of one divided by the number of years, and then subtracting one. Finally, multiplying by 100 converts it to a percentage.

CAGR is a useful measure for comparing the growth rates of different investments or assessing the performance of an investment over time. It smooths out the effects of volatility and provides a clearer picture of growth.

While CAGR is a valuable metric, it does not account for the risk or volatility of the investment. Therefore, it should be used alongside other metrics for a comprehensive analysis of investment performance.

Compound Annual Growth Rate (CAGR) Formula

\begin{gather*}\bold{Given{:}}\newline\begin{aligned}\text{Initial Value} &= \mathrm{IV}\newline\text{Final Value} &= \mathrm{FV}\newline\text{Time Period in Years} &= \mathrm{T}\end{aligned}\newline\bold{Calculate{:}}\newline\text{Compound Annual Growth Rate} = \mathrm{CAGR} \newline = ((\frac{\mathrm{FV}}{\mathrm{IV}})^{\frac{1}{\mathrm{T}}} - 1) \times \mathrm{100{\%}}\end{gather*}

Compound Annual Growth Rate (CAGR) Calculation Examples

Example 1

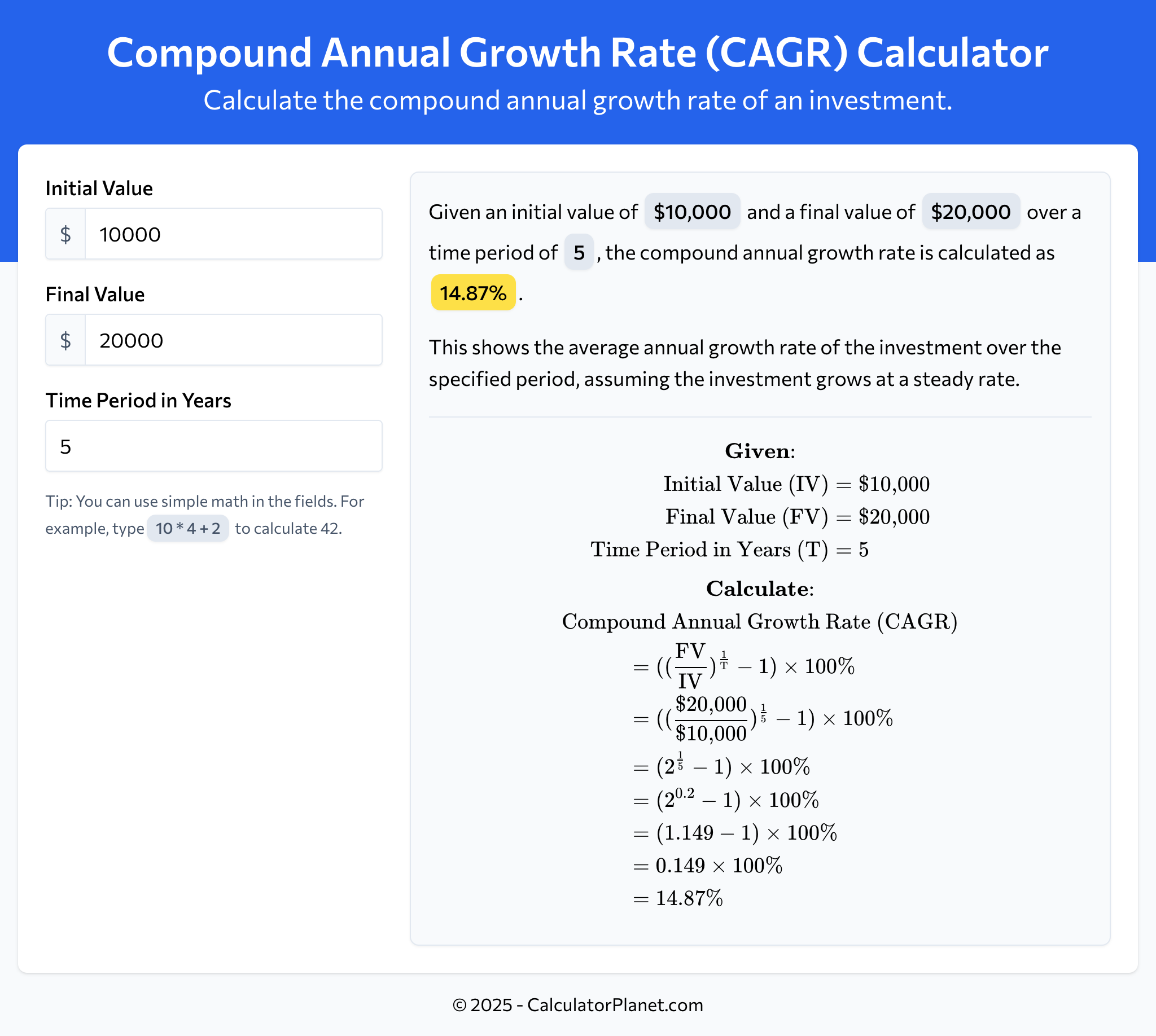
An investor purchases stocks for an initial value of $10,000. After 5 years, the value of the investment grows to $20,000.

Let's calculate the compound annual growth rate (CAGR) for this investment:

\begin{gather*}\bold{Given{:}}\newline\begin{aligned}\text{Initial Value}\space(\mathrm{IV}) &= \mathrm{{\$}10{,}000}\newline\text{Final Value}\space(\mathrm{FV}) &= \mathrm{{\$}20{,}000}\newline\text{Time Period in Years}\space(\mathrm{T}) &= 5\end{aligned}\newline\bold{Calculate{:}}\newline\text{Compound Annual Growth Rate}\space(\mathrm{CAGR})\newline\begin{aligned}&= ((\frac{\mathrm{FV}}{\mathrm{IV}})^{\frac{1}{\mathrm{T}}} - 1) \times \mathrm{100{\%}}\newline&= ((\frac{\mathrm{{\$}20{,}000}}{\mathrm{{\$}10{,}000}})^{\frac{1}{5}} - 1) \times \mathrm{100{\%}}\newline&= (2^{\frac{1}{5}} - 1) \times \mathrm{100{\%}}\newline&= (2^{0.2} - 1) \times \mathrm{100{\%}}\newline&= (1.149 - 1) \times \mathrm{100{\%}}\newline&= 0.149 \times \mathrm{100{\%}}\newline&= \mathrm{14.87{\%}}\end{aligned}\end{gather*}

This indicates that the compound annual growth rate for the investment over the 5 is 14.87%. This information can help the investor assess the performance of their investment strategy.

Example 2

A startup receives an initial investment of $5,000. After 3, the value of the startup increases to $15,000.

Let's calculate the CAGR for this startup's growth:

\begin{gather*}\bold{Given{:}}\newline\begin{aligned}\text{Initial Value}\space(\mathrm{IV}) &= \mathrm{{\$}5{,}000}\newline\text{Final Value}\space(\mathrm{FV}) &= \mathrm{{\$}15{,}000}\newline\text{Time Period in Years}\space(\mathrm{T}) &= 3\end{aligned}\newline\bold{Calculate{:}}\newline\text{Compound Annual Growth Rate}\space(\mathrm{CAGR})\newline\begin{aligned}&= ((\frac{\mathrm{FV}}{\mathrm{IV}})^{\frac{1}{\mathrm{T}}} - 1) \times \mathrm{100{\%}}\newline&= ((\frac{\mathrm{{\$}15{,}000}}{\mathrm{{\$}5{,}000}})^{\frac{1}{3}} - 1) \times \mathrm{100{\%}}\newline&= (3^{\frac{1}{3}} - 1) \times \mathrm{100{\%}}\newline&= (3^{0.333} - 1) \times \mathrm{100{\%}}\newline&= (1.442 - 1) \times \mathrm{100{\%}}\newline&= 0.442 \times \mathrm{100{\%}}\newline&= \mathrm{44.225{\%}}\end{aligned}\end{gather*}

This calculation shows that the compound annual growth rate for the startup over the 3 is 44.225%. This can guide future investment decisions and growth strategies.

Reference This Page

If you found our Compound Annual Growth Rate (CAGR) Calculator valuable, please consider referencing this page in your work. You can easily cite it by using the following formatted text:

<a href="https://calculatorplanet.com/finance/compound-annual-growth-rate">Compound Annual Growth Rate (CAGR) Calculator by Calculator Planet</a>

Compound Annual Growth Rate (CAGR) Calculator by CalculatorPlanet.com