Net Present Value (NPV) Calculator

Calculate the net present value to evaluate investment profitability and decision-making.

Please fill in all the fields.

What is Net Present Value (NPV)?

Net Present Value (NPV) is the difference between the present value of future cash flows and the initial investment.

NPV is calculated by discounting future cash flows to their present value and subtracting the initial investment, providing a dollar measure of value creation.

Understanding NPV is crucial for investment decision-making, as it indicates whether a project or investment will add value to the business.

A positive NPV indicates that the investment is expected to generate value and should be accepted, while a negative NPV suggests the investment should be rejected.

NPV accounts for the time value of money and uses the company’s cost of capital or required rate of return as the discount rate.

NPV is widely used in capital budgeting, project evaluation, and investment analysis across various industries and investment types.

While NPV is a powerful tool, it requires accurate cash flow projections and appropriate discount rate selection for reliable results.

Net Present Value (NPV) Formula

\begin{gather*}\bold{Given{:}}\newline\begin{aligned}\text{Future Value} &= \mathrm{FV}\newline\text{Initial Investment} &= \mathrm{IC}\newline\text{Discount Rate} &= \mathrm{r}\newline\text{Time Period in Years} &= \mathrm{t}\end{aligned}\newline\bold{Calculate{:}}\newline\text{Net Present Value} = \mathrm{NPV} \newline = \frac{\mathrm{FV}}{(1 + \frac{\mathrm{r}}{\mathrm{100{\%}}})^{\mathrm{t}}} - \mathrm{IC}\end{gather*}

Net Present Value (NPV) Calculation Examples

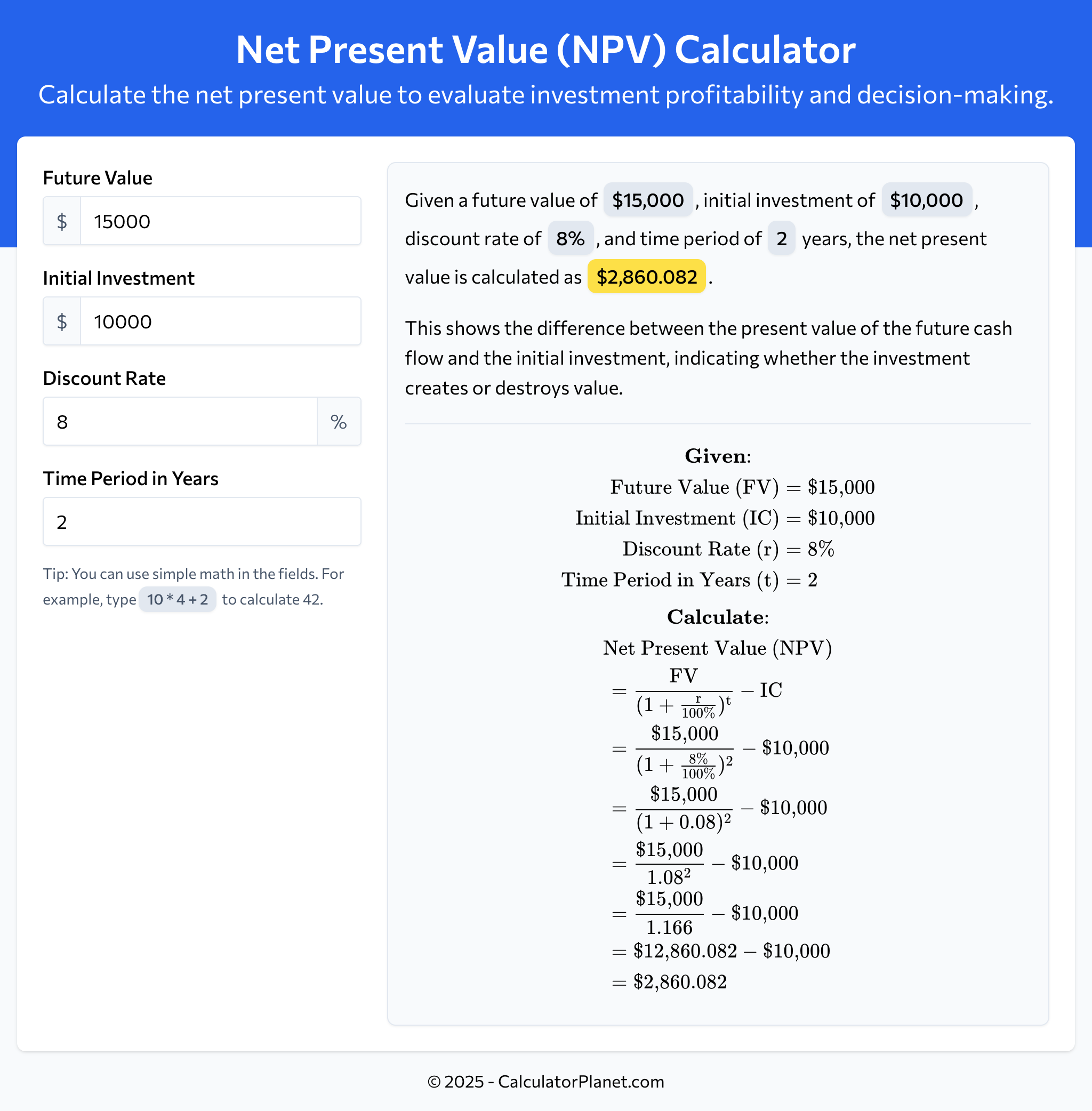
Example 1

A company is considering an investment that requires an initial outlay of $10,000 and will generate cash flow of $15,000 in 2 years. The company's cost of capital is 8%.

To evaluate this investment opportunity:

\begin{gather*}\bold{Given{:}}\newline\begin{aligned}\text{Future Value}\space(\mathrm{FV}) &= \mathrm{{\$}15{,}000}\newline\text{Initial Investment}\space(\mathrm{IC}) &= \mathrm{{\$}10{,}000}\newline\text{Discount Rate}\space(\mathrm{r}) &= \mathrm{8{\%}}\newline\text{Time Period in Years}\space(\mathrm{t}) &= 2\end{aligned}\newline\bold{Calculate{:}}\newline\text{Net Present Value}\space(\mathrm{NPV})\newline\begin{aligned}&= \frac{\mathrm{FV}}{(1 + \frac{\mathrm{r}}{\mathrm{100{\%}}})^{\mathrm{t}}} - \mathrm{IC}\newline&= \frac{\mathrm{{\$}15{,}000}}{(1 + \frac{\mathrm{8{\%}}}{\mathrm{100{\%}}})^{2}} - \mathrm{{\$}10{,}000}\newline&= \frac{\mathrm{{\$}15{,}000}}{(1 + 0.08)^{2}} - \mathrm{{\$}10{,}000}\newline&= \frac{\mathrm{{\$}15{,}000}}{1.08^{2}} - \mathrm{{\$}10{,}000}\newline&= \frac{\mathrm{{\$}15{,}000}}{1.166} - \mathrm{{\$}10{,}000}\newline&= \mathrm{{\$}12{,}860.082} - \mathrm{{\$}10{,}000}\newline&= \mathrm{{\$}2{,}860.082}\end{aligned}\end{gather*}

The net present value is $2,860.082, indicating that this investment creates value since the NPV is positive.

A positive NPV suggests that the investment will generate returns exceeding the required rate of return, making it financially attractive.

Example 2

An investor is evaluating a project requiring an initial investment of $15,000 that will return $12,000 in 3 years. The required rate of return is 10%.

Let's calculate the NPV to determine if this investment is worthwhile:

\begin{gather*}\bold{Given{:}}\newline\begin{aligned}\text{Future Value}\space(\mathrm{FV}) &= \mathrm{{\$}12{,}000}\newline\text{Initial Investment}\space(\mathrm{IC}) &= \mathrm{{\$}15{,}000}\newline\text{Discount Rate}\space(\mathrm{r}) &= \mathrm{10{\%}}\newline\text{Time Period in Years}\space(\mathrm{t}) &= 3\end{aligned}\newline\bold{Calculate{:}}\newline\text{Net Present Value}\space(\mathrm{NPV})\newline\begin{aligned}&= \frac{\mathrm{FV}}{(1 + \frac{\mathrm{r}}{\mathrm{100{\%}}})^{\mathrm{t}}} - \mathrm{IC}\newline&= \frac{\mathrm{{\$}12{,}000}}{(1 + \frac{\mathrm{10{\%}}}{\mathrm{100{\%}}})^{3}} - \mathrm{{\$}15{,}000}\newline&= \frac{\mathrm{{\$}12{,}000}}{(1 + 0.1)^{3}} - \mathrm{{\$}15{,}000}\newline&= \frac{\mathrm{{\$}12{,}000}}{1.1^{3}} - \mathrm{{\$}15{,}000}\newline&= \frac{\mathrm{{\$}12{,}000}}{1.331} - \mathrm{{\$}15{,}000}\newline&= \mathrm{{\$}9{,}015.778} - \mathrm{{\$}15{,}000}\newline&= \mathrm{-{\$}5{,}984.222}\end{aligned}\end{gather*}

The net present value is -$5,984.222, indicating that this investment destroys value since the NPV is negative.

A negative NPV suggests that the investment will not generate sufficient returns to meet the required rate of return, making it an unattractive investment.

Reference This Page

If you found our Net Present Value (NPV) Calculator valuable, please consider referencing this page in your work. You can easily cite it by using the following formatted text:

<a href="https://calculatorplanet.com/finance/net-present-value">Net Present Value (NPV) Calculator by Calculator Planet</a>

Net Present Value (NPV) Calculator by CalculatorPlanet.com