Buying Power Calculator

Calculate money's purchasing power over time due to inflation.

Please fill in all the fields.

What is Buying Power?

Buying power refers to the amount of goods or services that can be purchased with a unit of currency.

Buying power is influenced by inflation, which erodes the value of money over time. As prices rise, the same amount of money buys fewer goods and services.

Understanding buying power helps individuals make informed decisions about savings, investments, and spending. It allows people to assess how much their money will be worth in the future, aiding in financial planning.

Buying power is a crucial concept in personal finance, economics, and investment strategies.

Buying Power Formula

\begin{gather*}\bold{Given{:}}\newline\begin{aligned}\text{Amount of Money} &= \mathrm{A}\newline\text{Inflation Rate} &= \mathrm{IR}\newline\text{Number of Years} &= \mathrm{Y}\end{aligned}\newline\bold{Calculate{:}}\newline\text{Purchasing Power} = \mathrm{PP} \newline = \frac{\mathrm{A}}{(1 + \frac{\mathrm{IR}}{\mathrm{100{\%}}})^{\mathrm{Y}}}\end{gather*}

Buying Power Calculation Examples

Example 1

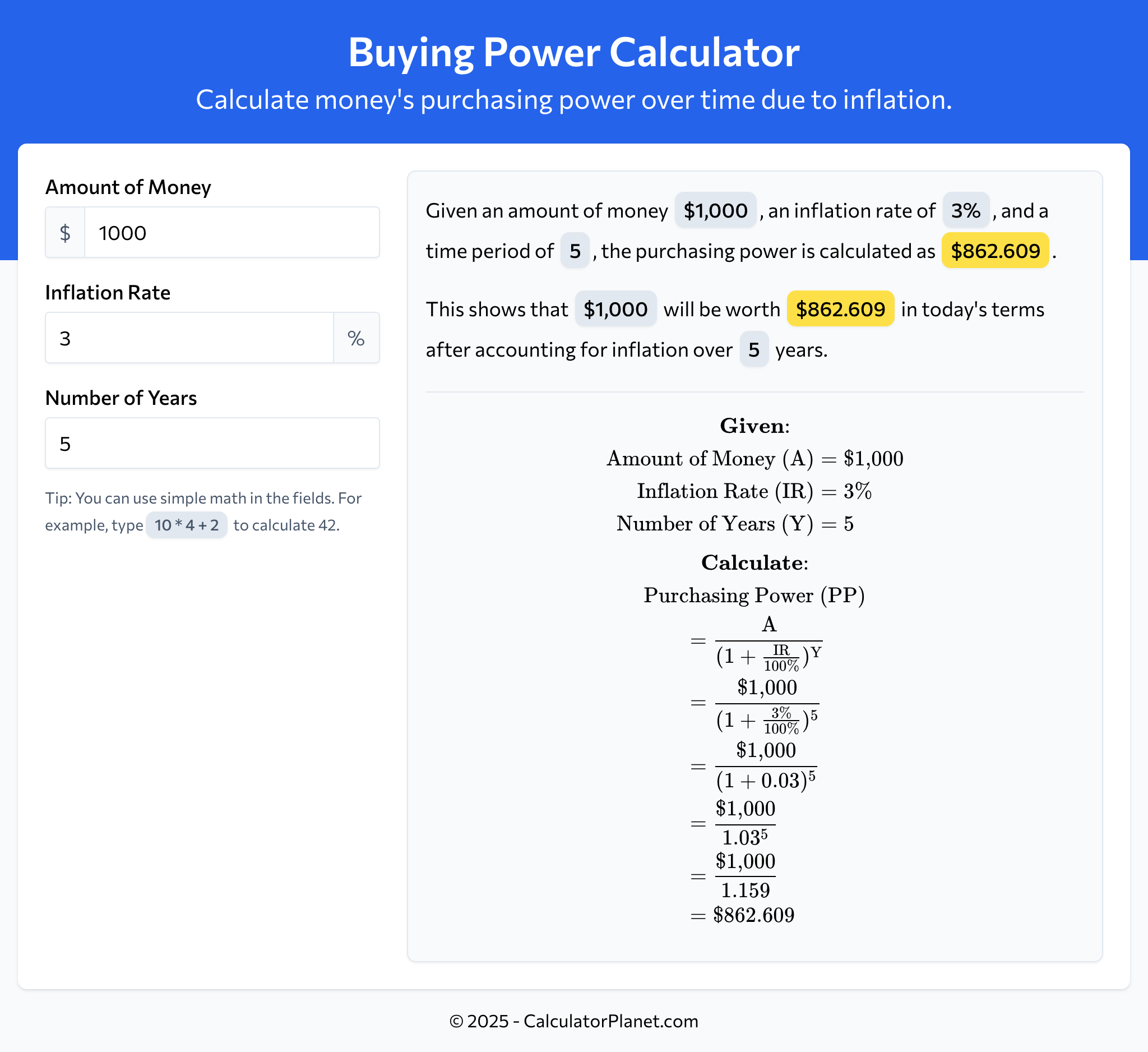
A consumer has an amount of $1,000 today. They want to know how much this amount will be worth in terms of purchasing power after 5 years, considering an inflation rate of 3%.

Let's calculate the purchasing power:

\begin{gather*}\bold{Given{:}}\newline\begin{aligned}\text{Amount of Money}\space(\mathrm{A}) &= \mathrm{{\$}1{,}000}\newline\text{Inflation Rate}\space(\mathrm{IR}) &= \mathrm{3{\%}}\newline\text{Number of Years}\space(\mathrm{Y}) &= 5\end{aligned}\newline\bold{Calculate{:}}\newline\text{Purchasing Power}\space(\mathrm{PP})\newline\begin{aligned}&= \frac{\mathrm{A}}{(1 + \frac{\mathrm{IR}}{\mathrm{100{\%}}})^{\mathrm{Y}}}\newline&= \frac{\mathrm{{\$}1{,}000}}{(1 + \frac{\mathrm{3{\%}}}{\mathrm{100{\%}}})^{5}}\newline&= \frac{\mathrm{{\$}1{,}000}}{(1 + 0.03)^{5}}\newline&= \frac{\mathrm{{\$}1{,}000}}{1.03^{5}}\newline&= \frac{\mathrm{{\$}1{,}000}}{1.159}\newline&= \mathrm{{\$}862.609}\end{aligned}\end{gather*}

This indicates that after 5 years, the purchasing power of $1,000 will be equivalent to $862.609 in today's dollars, reflecting the impact of 3% inflation.

Example 2

An investor has $500 saved up. They are curious about the future purchasing power of this amount after 10 years, with an expected inflation rate of 2%.

Let's calculate the purchasing power:

\begin{gather*}\bold{Given{:}}\newline\begin{aligned}\text{Amount of Money}\space(\mathrm{A}) &= \mathrm{{\$}500}\newline\text{Inflation Rate}\space(\mathrm{IR}) &= \mathrm{2{\%}}\newline\text{Number of Years}\space(\mathrm{Y}) &= 10\end{aligned}\newline\bold{Calculate{:}}\newline\text{Purchasing Power}\space(\mathrm{PP})\newline\begin{aligned}&= \frac{\mathrm{A}}{(1 + \frac{\mathrm{IR}}{\mathrm{100{\%}}})^{\mathrm{Y}}}\newline&= \frac{\mathrm{{\$}500}}{(1 + \frac{\mathrm{2{\%}}}{\mathrm{100{\%}}})^{10}}\newline&= \frac{\mathrm{{\$}500}}{(1 + 0.02)^{10}}\newline&= \frac{\mathrm{{\$}500}}{1.02^{10}}\newline&= \frac{\mathrm{{\$}500}}{1.219}\newline&= \mathrm{{\$}410.174}\end{aligned}\end{gather*}

This calculation shows that in 10 years, the purchasing power of $500 will be reduced to $410.174, illustrating the effect of 2% inflation over time.

Reference This Page

If you found our Buying Power Calculator valuable, please consider referencing this page in your work. You can easily cite it by using the following formatted text:

<a href="https://calculatorplanet.com/finance/buying-power">Buying Power Calculator by Calculator Planet</a>

Buying Power Calculator by CalculatorPlanet.com